abcjilo.blogg.se - Example of reflection over y axis

#Example of reflection over y axis how to

Now, by counting the distance between these two points, you should get the answer of 8 units. Let's pick the origin point for these functions, as it is the easiest point to deal with. The best way to practice finding the axis of symmetry is to do an example problem:įind the axis of symmetry for the two functions show in the image below.Īgain, all we need to do to solve this problem is to pick the same point on both functions, count the distance between them, and divide by 2. This is because, by it's definition, an axis of symmetry is exactly in the middle of the function and its reflection. In this case, all we have to do is pick the same point on both the function and its reflection, count the distance between them, and divide that by 2. It can be the y-axis, or any vertical line with the equation x = constant, like x = 2, x = -16, etc.įinding the axis of symmetry, like plotting the reflections themselves, is also a simple process. The axis of symmetry is simply the vertical line that we are performing the reflection across.

#Example of reflection over y axis how to

But before we go into how to solve this, it's important to know what we mean by "axis of symmetry". In some cases, you will be asked to perform vertical reflections across an axis of symmetry that isn't the y-axis. Step 3: Divide these points by (-1) and plot the new pointsįor a visual tool to help you with your practice, and to check your answers, check out this fantastic link here. Step 2: Identify easy-to-determine points

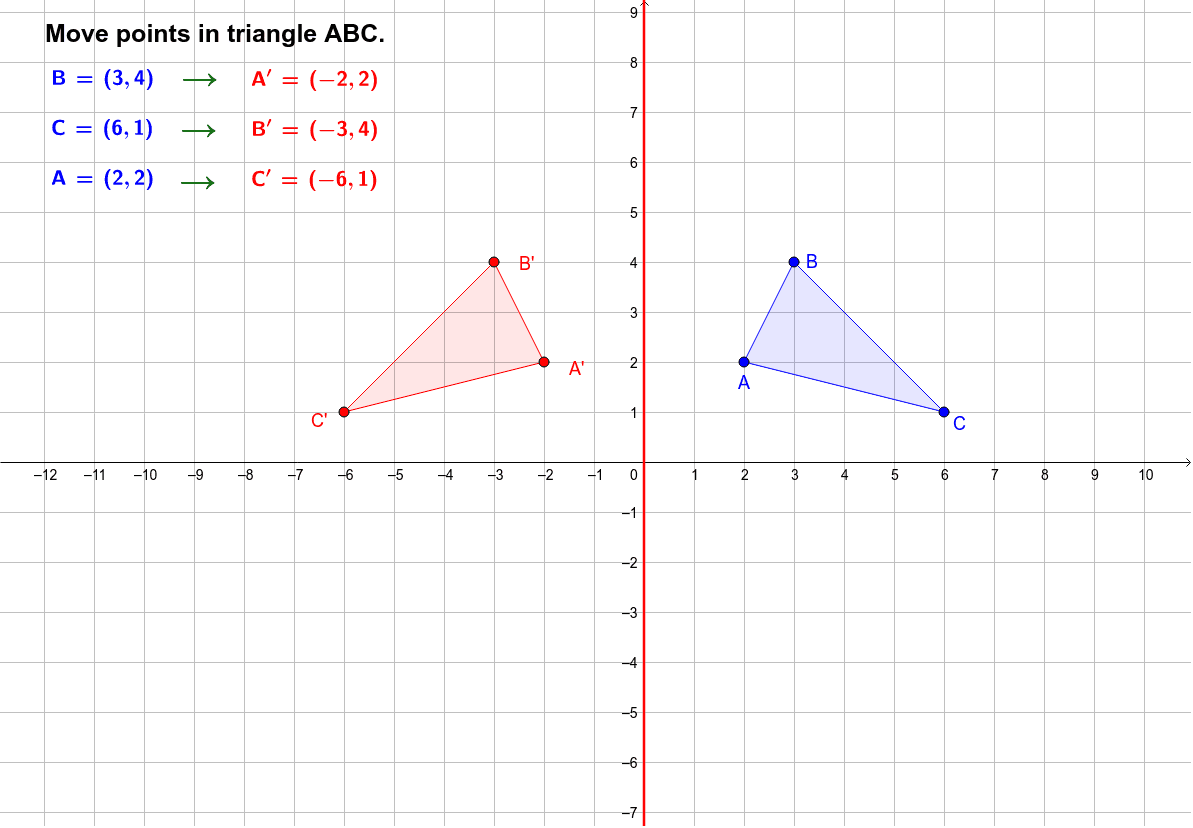
Step 1: Know that we're reflecting across the y-axis Below are several images to help you visualize how to solve this problem. Don't pick points where you need to estimate values, as this makes the problem unnecessarily hard. When we say "easy-to-determine points" what this refers to is just points for which you know the x and y values exactly. Remember, the only step we have to do before plotting the f(-x) reflection is simply divide the x-coordinates of easy-to-determine points on our graph above by (-1). Given the graph of y = f ( x ) y=f(x) y = f ( x ) as shown, sketch y = f ( − x ) y = f(-x) y = f ( − x ). The best way to practice drawing reflections over y axis is to do an example problem: In order to do this, the process is extremely simple: For any function, no matter how complicated it is, simply pick out easy-to-determine coordinates, divide the x-coordinate by (-1), and then re-plot those coordinates.

Graph y = f ( − x ) y = f(-x) y = f ( − x ).

In a potential test question, this can be phrased in many different ways, so make sure you recognize the following terms as just another way of saying "perform a reflection across the y-axis": One of the most basic transformations you can make with simple functions is to reflect it across the y-axis or another vertical axis. The reflection of a point $(x,y)$ over the x-axis will be represented as $(x,-y)$.Īllan was working as an architect engineer on a construction site and he just realized that the function $y = 3x^+4(-x) -1)$.Before we get into reflections across the y axis, make sure you've refreshed your memory on how to do simple vertical translation and horizontal translation. In that case, the reflection over the x-axis equation for the given function will be written as $y = -f(x)$, and here you can see that all the values of “$y$” will have an opposite sign as compared to the original function. When we have to reflect a function over the x-axis, the points of the x coordinates will remain the same while we will change the signs of all the coordinates of the y-axis.įor example, suppose we have to reflect the given function $y = f(x)$ around the x-axis.

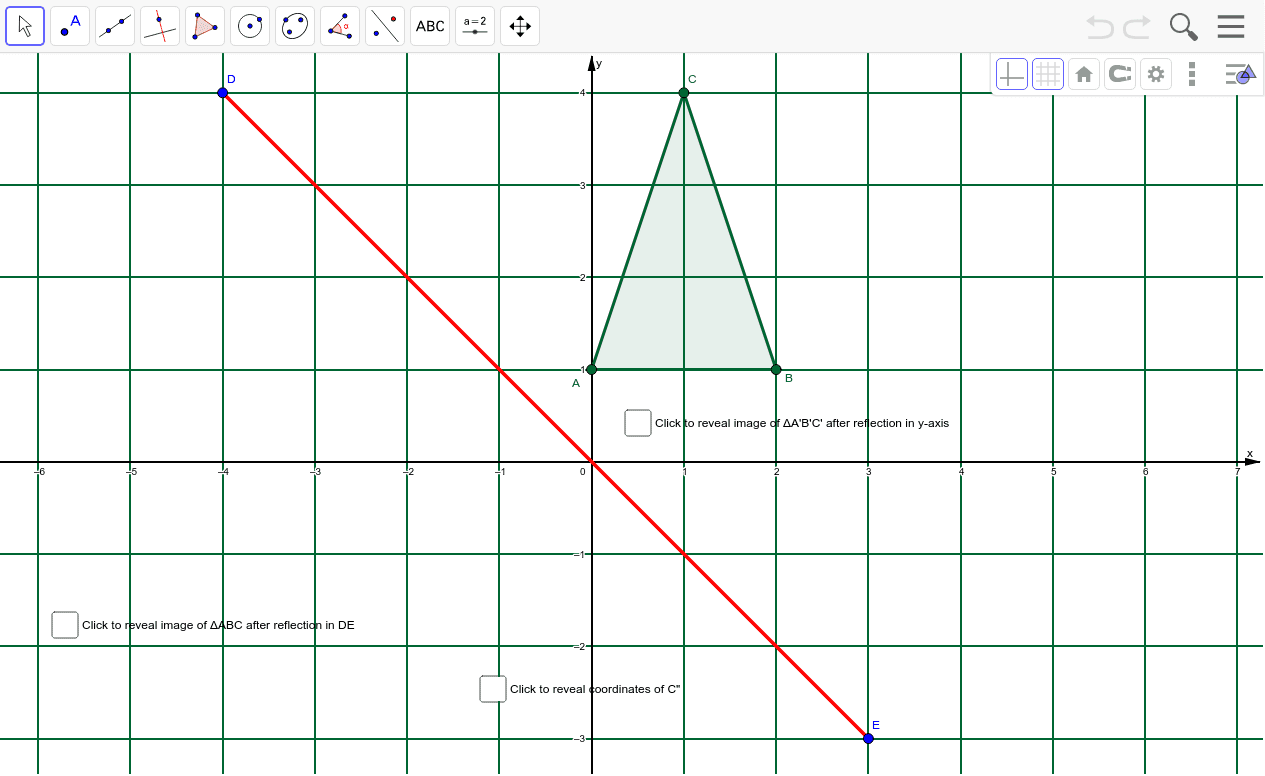
How To Reflect a Function Over the X-axis Reflection of a function over x and y axisĪll these types of reflections can be used for reflecting linear functions and non-linear functions.Reflection of a function over y- axis or horizontal reflection.Reflection of a function over x – axis or vertical reflection.Hence, we classify reflections of the function as: Consider the function $y = f(x)$, it can be reflected over the x-axis as $y = -f(x)$ or over the y-axis as $y = f(-x)$ or over both the axis as $y = -f(-x)$.

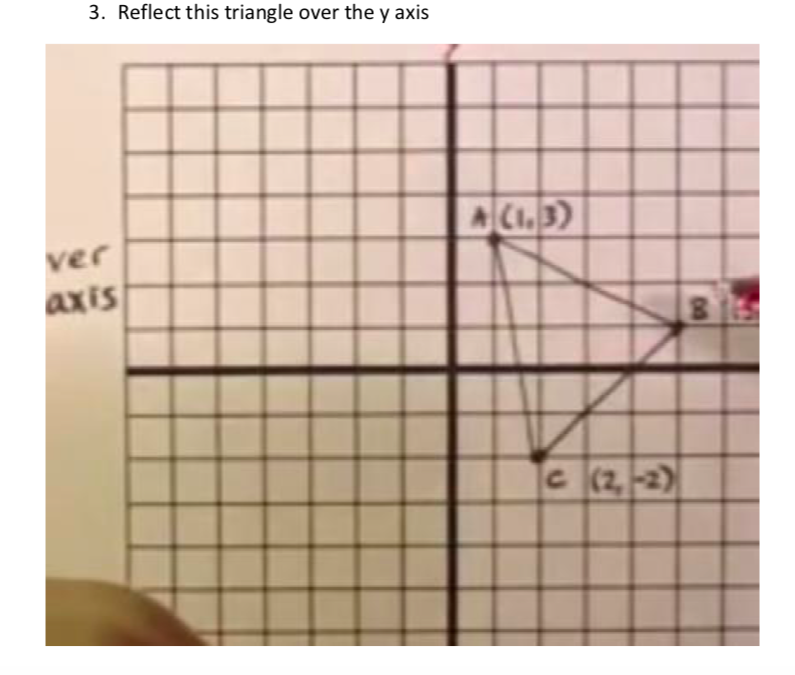
There are three types of reflections of a function. Read more How Hard is Calculus? A Comprehensive Guide